Question

Divide f(x) by g(x) using long division and write the result using the division algorithm. Please help!

Answer 1

To use long division in polynomials, we follow steps similar to normal long division, but we look for the terms from higher degree to lower.

We are dividing:

`4x^3-7x^2+3`

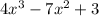
By:

`2x-1`

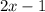
We want to multiply the divisor by some expression that will make the higher term equal to the higher term of the dividend. The higher term of the dividend is 4x³, to get to that, we can multiply the divisor by 2x²:

`2x^2(2x-1)=2x^2\cdot2x-2x^2=4x^3-2x^2`

Now we have the same term, so we just substract what we have got from the dividend:

`\begin{gathered} 4x^3-7x^2+3 \\ -(4x^3-2x^2) \\ \\ 4x^3-4x^3-7x^2+2x^2+3 \\ -5x^2+3 \end{gathered}`

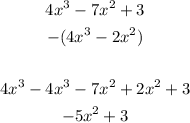
Notice that we don't have a third degree term anymore.

So, until now we have done:

- Multiplied the divisor by 2x²

- Got a remainder of -5x² + 3

Now, we just repeat with the remainder.

We want to multiply 2x - 1 so that the higher term is -5x², so we can multiply by -5x/2:

`-(5x)/(2)(2x-1)=-(5x\cdot2x)/(2)+(5x)/(2)=-5x^2+(5x)/(2)`

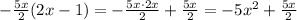
And we do the substraction:

`\begin{gathered} -5x^2+3 \\ -(-5x^2+(5x)/(2)) \\ \\ -5x^2+5x^2-(5x)/(2)+3 \\ -(5x)/(2)+3 \end{gathered}`

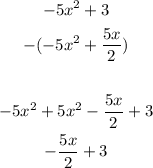
So, now we have got:

- Multiplied the divisor by 2x² and then by -5x/2

- Got a remainder of -5x/2 + 3

Now, we repeat once more:

To get -5x/2, we multiply the divisor by -5/4:

`-(5)/(4)(2x-1)=-(5\cdot2x)/(4)+(5)/(4)=-(5x)/(2)+(5)/(4)`

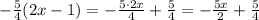
And we substract from the remainder:

`\begin{gathered} -(5x)/(2)+3 \\ -(-(5x)/(2)+(5)/(4)) \\ \\ -(5x)/(2)+(5x)/(2)+3-(5)/(4) \\ (12-5)/(4) \\ (7)/(4) \end{gathered}`

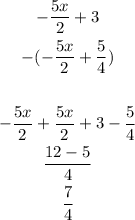
So, we have done:

- Multiplied the divisor by 2x² then -5x/2 then -5/4

- Got a remainder of 7/4

This means that th result of the division is:

`2x^2-(5x)/(2)-(5)/(4)`

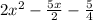
And the remainder is:

`(7)/(4)`

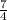
But, the answer wants us to write what the dividend is equal to.

Let's write first in the division form:

`(4x^3-7x^2+3)/(2x-1)=2x^2-(5x)/(2)-(5)/(4)+((7)/(4))/(2x-1)`

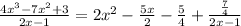
Notice that we result is the quotient plus the remainder divided by the divisor.

If we multiply both sides by the divisor, we will get:

`4x^3-7x^2+3=(2x-1)\mleft(2x^2-(5x)/(2)-(5)/(4)\mright)+(7)/(4)`

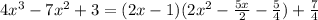
That is the answer.