Question

4.) A plane flies 990 miles with the wind in 2.75 hours. It would takethe plane 3.5 hours to fly 1099 miles against the same wind speed.Find the speed of the plane with no wind and the speed of the wind.SET UP a system of linear equations using two variables. SOLVEthe system to answer the problem. SHOW ALL STEPS!! (10 pts)

Answer 1

Step 1 :

In this question, we were given that a plane flies 990 miles with the wind in 2.75 hours.

It would take the plane 3.5 hours to fly 1099 miles against the same wind speed.

Find the speed of the plane with no wind and the speed of the wind.

Step 2 :

The system of Linear Equations using the two variables are as follows:

`u\text{ + v = }\frac{990}{2.\text{ 75 }}\text{ = 360 --- equ 1}`
`u\text{ - v = }\frac{1099}{3.5\text{ }}\text{ = 314 -- equ 2}`

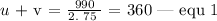
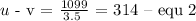
Step 3 :

Solving the two systems of equations, using elimination method:

`\begin{gathered} equ\text{ 1 + equ 2 : } \\ 2\text{ u = 360 + 314} \\ 2u\text{ = 674} \\ \text{Divide both sides by 2 , we have that:} \\ u\text{ =}(674)/(2)\text{ = 337 miles per hour} \end{gathered}`

Put the value of u = 337 miles per hour in equ 1 , we have that:

`\begin{gathered} u\text{ + v = 360 -- equ 1} \\ 337\text{ + v = 360} \\ \text{v = 360 - 337} \\ \text{v = 23 miles per hour} \end{gathered}`

CONCLUSION:

The speed of the plane with no wind, u = 337 miles per hour

The speed of the wind, v = 23 miles per hour.