To answer this question, we can use one of the trigonometric ratios since we have a right triangle here. We also need to know that the reference angle is Having this information into account, we can use the following trigonometric ratio:

That is, we have the value of the opposite side, and we will have the value for tan(5). Then, we have:
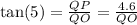
Now, we have to solve the equation for QO:
1. Multiply each side of the equation by QO:

2. Divide both sides of the equation by tan(5):
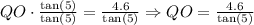
Therefore, we have that QO is:
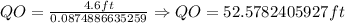
If we rounded this value to the nearest tenth, we have that QO = 52.6 ft.