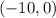Question

what is the equation of a circle with center (-1, -2) and passes through the point (6, 4)? which of the following points is also located on the circle?(6, -6) (-10, 0)(-6, 4)

Answer 1

The equation of the circle is;

`(x+1)^2+(y+2)^2=85`

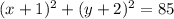
The point that is located on the circle is;

`(-10,0)`

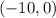
Step-by-step explanation:

Given that the circle has its center at (-1, -2) and passes through the point (6, 4);

`\begin{gathered} (h,k)=(-1,-2) \\ (x,y)=(6,4) \end{gathered}`

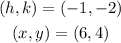
Recall that the equation of a circle can be written as;

`(x-h)^2+(y-k)^2=r^2`

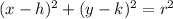
To get r, let us substitute the given values into the equation;

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (6-(-1))^2+(4-(-2))^2=r^2 \\ (6+1)^2+(4+2)^2=r^2_{} \\ 7^2+6^2=r^2 \\ 49+36=r^2 \\ 85=r^2 \\ r=\sqrt[]{85} \end{gathered}`

Therefore, the equation of the circle can be written as;

`\begin{gathered} (x-h)^2+(y-k)^2=r^2 \\ (x-(-1))^2+(y-(-2))^2=(\sqrt[]{85})^2 \\ (x+1)^2+(y+2)^2=85 \end{gathered}`

The equation of the circle is;

`(x+1)^2+(y+2)^2=85`

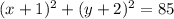
We want to confirm which of the given points is located on the circle.

Plotting the graph of the circle;

From the graph of the equation of the circle and the given points as shown above.

We can observe that the only point that is located on the line of the circle is;

`(-10,0)`

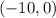
Therefore, the point that is located on the circle is;

`(-10,0)`