Question

Find all the roots of the equation x4 - 2x3 + 14x2 - 18x + 45 = 0 given that 1 + 2i is one of its roots.

Answer 1

1+3=5x3, 5xp, =3 roots because of all of its roots divided

Answer 2

another three roots are 1-2i, 3i ,-3i

Explanation:

`2x^3+14x^2-18x+45 = 0`

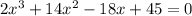
has one root = 1+2i

then another root will be = 1-2i [ since complex roots always occurs in pair]

therefore together both roots makes function as

`(x-1+2i) (x-1-2i) =0 \\(x-1)^2=-4 \\(x^2-2x+1=-4\\(x^2-2x+5)=0`

since this polynomial is formed by its roots so it must divide the parent polynomial therefore on dividing the parent polynomial by obtained polynomial, we get

`x^2+9 = 0 \\x^2 = -9 \\x = +3i \\x =-3i`

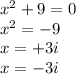
therefore we have three other roots are

1-2i

-3i

3i