Question

Find x and y . Approximate your answer to one decimal place. I used comma for decimal separation. A random variable X has as a range of values the values 1, 2 and 3 with probabilities P (X = 1) = 0.2, P (X = 2) = x, and P (X = 3) = y. If Var (X) = 0.29, then x = and y =

Answer 1

We have a random discrete variable X, that takes values 1, 2 and 3.

As the probabilities of all the sample space is equal to 1.

So then we can define x in function of y:

`\begin{gathered} P(x=1)+P(x=2)+P(x=3)=1 \\ 0.2+x+y=1 \\ y=1-0.2-x \\ y=0.8-x \end{gathered}`

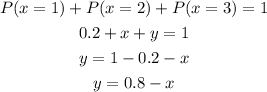
We can start by calculating the mean of X as:

`\begin{gathered} \mu=\sum ^3_(i\mathop=1)p_i\cdot x_i \\ \mu=0.2\cdot1+x\cdot2+y\cdot3 \\ \mu=0.2+2x+3(0.8-x) \\ \mu=0.2+2x+2.4-3x \\ \mu=2.6-x \end{gathered}`

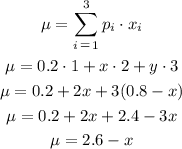
We can write the variance of X as:

`\begin{gathered} \sigma^2=\sum ^3_(i\mathop=1)p_i\cdot(x_i-\mu)^2 \\ \sigma^2=0.2\cdot(1-(2.6-x))^2+x\cdot(2-(2.6-x))^2+(0.8-x)\cdot(3-(2.6-x))^2 \\ \sigma^2=0.2\cdot(x-1.6)^2+x\cdot(x-0.6)^2+(0.8-x)\cdot(x+0.4)^2 \\ \sigma^2=0.2\cdot(x^2-3.2x+2.56)+x\cdot(x^2-1.2x+0.36)+(0.8-x)(x^2+0.8x+0.16) \\ \sigma^2=0.2x^2-0.64x+0.512+x^3-1.2x^2+0.36x+0.8x^2+0.64x+0.128-x^3-0.8x^2-0.16x \\ \sigma^2=(1-1)x^3+(0.2-1.2+0.8-0.8)x^2+(-0.64+0.36+0.64-0.16)x+(0.512+0.128) \\ \sigma^2=-x^2+0.2x+0.64 \end{gathered}`

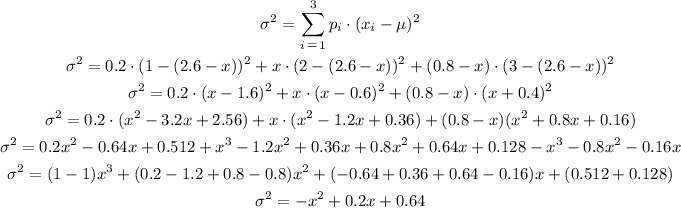
As the variance, σ², is equal to 0.29, then we can find the possible values for x as:

`\begin{gathered} \sigma^2=0.29 \\ -x^2+0.2x+0.64=0.29 \\ -x^2+0.2x+0.64-0.29=0 \\ -x^2+0.2x+0.35=0 \\ x^2-0.2x-0.35=0 \end{gathered}`

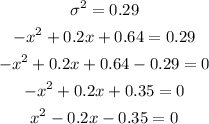
We can find the roots of this equation as:

`\begin{gathered} x=\frac{-(-0.2)\pm\sqrt[]{(-0.2)^2-4\cdot1\cdot(-0.35)}}{2\cdot1} \\ x=\frac{0.2\pm\sqrt[]{0.04+1.4}}{2} \\ x=\frac{0.2\pm\sqrt[]{1.44}}{2} \\ x=(0.2\pm1.2)/(2) \\ x_1=(0.2-1.2)/(2)=-(1)/(2)=-0.5 \\ x_2=(0.2+1.2)/(2)=(1.4)/(2)=0.7 \end{gathered}`

The value of x = -0.5, as it is a probability, has to have a value of between 0 and 1, is not valid.

Then, the only valid value for x is x = 0.7.

We then can calculate y as:

`y=0.8-x=0.8-0.7=0.1`

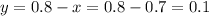
Answer: x = 0.7 and y = 0.1