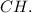The empirical formula for a compound with 92.25% carbon and 7.75% hydrogen is CH, indicating a 1:1 ratio. This formula represents the simplest whole number ratio of carbon to hydrogen.
To find the empirical formula of a compound, you need to determine the mole ratios of each element in the compound. Start by assuming you have 100 grams of the compound, and then determine the moles of each element based on the given percentages.
Given percentages:
- Carbon (C): 92.25%
- Hydrogen (H): 7.75%
Assume 100 g of the compound, then:
1. Convert percentages to grams:
-
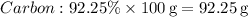
-
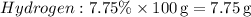
2. Convert grams to moles using the molar mass:
- The molar mass of carbon (C) is approximately 12 g/mol.
- The molar mass of hydrogen (H) is approximately 1 g/mol.
-
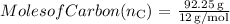
-
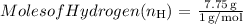
3. Determine the simplest whole number ratio:
- Divide the moles of each element by the smallest number of moles obtained.
![\[ \text{Empirical ratio} = \frac{n_{\text{C}}}{n_{\text{H}}} \]](https://img.qammunity.org/2022/formulas/chemistry/high-school/cgstyn9kgfa901de4e3h0ja49ito6b0bu5.png)
4. Write the empirical formula using the ratios:
- The empirical formula is often written with subscripts as the ratio of moles.
Now, let's calculate:
![\[\text{Empirical ratio} = (92.25 / 12)/(7.75 / 1)\]](https://img.qammunity.org/2022/formulas/chemistry/high-school/38azwpvsvthfmdhlfbaxl5r0nsx4p8hll7.png)
![\[\text{Empirical ratio} \approx (7.6875)/(7.75)\]](https://img.qammunity.org/2022/formulas/chemistry/high-school/7y9kgp9w17eozlshx8m3uj560mv77rkree.png)
![\[\text{Empirical ratio} \approx 0.992\]](https://img.qammunity.org/2022/formulas/chemistry/high-school/a1bw4geec60vlrxp2h1htakcofsa810orr.png)
Since we want a whole number ratio, we can multiply both the numerator and denominator by a common factor to obtain whole numbers. In this case, multiplying by 4 gives:
![\[\text{Empirical ratio} = (4 * 7.6875)/(4 * 7.75) = (30.75)/(31)\]](https://img.qammunity.org/2022/formulas/chemistry/high-school/xgi2f98vtr83u02rahodfn9j5kg7wowfdn.png)
So, the empirical formula is approximately
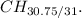
However, it's conventional to round to the nearest whole number, so the empirical formula is