Question

Fitzwilliam is buying a new car. The sticker price for the base model is $10,000,but the options he wants will cost him an extra 15%. He then talks the dealer intogiving him 10% off. Fitzwilliam has also decided to put down a 25% downpayment on the car.Find Fitzwilliam's down payment on the car.Find the balance that Fitzwilliam needs to finance.Fitzwilliam has three options for financing for the balance on the car: thedealership, the bank, or his parents.Through the dealership he can get a 60 month, 5% APR monthly installmentloan.o The bank will offer Fitzwilliam a 5.5% APR monthly installment loan for 48months.His parents would loan him the money and he would need to pay it all backafter 15 months with 20% (simple) interest.Find Fitzwilliam's monthly payment on the dealership loan.Find Fitzwilliam's monthly payment on the bank loan.Find the amount Fitzwilliam would owe his parents after 15 months.Find the amount of interest that Fitzwilliam would need to pay on eachloan.Which option would you suggest for Fitzwilliam? Justify your choice.

Answer 1

We have to start by finding the actual price he is paying.

We start with a base price of $10,000.

With the custom options, the price rises by 15%, so it will be 1.15 times the base price:

`1.15\cdot10000=11500`

After that, he obtains a 10% off, so the final price will be 100-10 = 90% of the last price:

`11500\cdot0.90=10350`

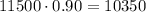
He does a downpayment of 25%, so we can calculate the downpayment using this last calculated price:

`dp=0.25\cdot10350=2587.50`

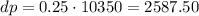
The remaining 75% will be the balance to be financed. This amount will represent:

`bal=0.75\cdot10350=7762.50`

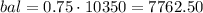
We have 3 options to finance the balance. We will analyze each one.

a) The dealership offers a 60 month financing with 5% APR.

The APR is the nominal annula interest rate, so we can divide 60 months as n = 5 years with a subperiod m = 12.

We can now relate the balance to the monthly payment using the annuity formula as:

`\begin{gathered} M=((r)/(m)\cdot PV)/(1-(1+(r)/(m))^(-n\cdot m)) \\ \\ M=((0.05)/(12)\cdot7762.50)/(1-(1+(0.05)/(12))^(-5\cdot12)) \\ \\ M\approx(0.004167\cdot7762.50)/(1-(1.004167)^(-60)) \\ \\ M\approx(32.34375)/(1-0.77921) \\ \\ M\approx(32.34375)/(0.22079) \\ \\ M\approx146.49 \end{gathered}`

The monthly payment is $146.49.

b) In this case for the bank is a similar calculation, but with APR = 5.5% and 48 months instead of 60 months.

We then can calculate the monthly payments as:

`\begin{gathered} M=((r)/(m)PV)/(1-(1+(r)/(m))^(-n*m)) \\ \\ M=((0.055)/(12)*7762.50)/(1-(1+(0.055)/(12))^(-48)) \\ \\ M\approx(35.578125)/(1-0.802922) \\ \\ M\approx(35.578125)/(0.197078) \\ \\ M\approx180.53 \end{gathered}`

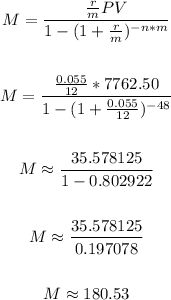
The monthly payment is $180.53.

c) The last option has a 20% simple interest and a period of 15 months.

We can use the formula to calculate the final payment after 15 months as:

`\begin{gathered} FV=PV(1+i*n) \\ FV=7762.50(1+0.2*(15\/12)) \\ FV=7762.50(1.25) \\ FV=9703.125 \end{gathered}`

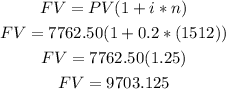
He would owe them $9703.13.

d) We have to choose which one option is better.

Between the dealership deal and the bank loan, the former offers a longer period and less APR, so it is better in all senses to the bank loan.

We can now compare it to the parents loan.

We can calculate the total amount he will pay for the dealership loan as:

`\begin{gathered} T=P*n*m \\ T=146.49*60 \\ T=8789.40 \end{gathered}`

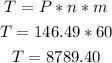
He will pay less than with the parents loan. Besides a longer period for financing, the total interest paid is lower.

Then,the dealership deal is the better option.

Answer:

1. Downpayment: $2587.50

2. Balance: $7762.50

3.a. Monthly payment (dealership): $146.49

3. b. Monthly payment (bank): $180.53

3.c. Amount owed: $970.13

3.d. The dealership deal is the better option.