Question

Consider the function: F(x) = x^2 - 4x +1a) Simplify the expression : f(x+h) - f(x) / h , for the given function.b) What will happen to the expression in part a when h becomes very close to zero?c) Use the simplified expression from part a to estimate the instantaneous rate of change at: x=1 , x=2, and x=3. Explain what these results tell you about the function.

Answer 1

`\begin{gathered} a)2x+h-4 \\ b)\lim _(h\to0)2x-4 \\ c)x=-1,f^(\prime)(1)=-2 \\ x=2,f^(\prime)(2)=0 \\ x=3,f^(\prime)(3)=2 \end{gathered}`

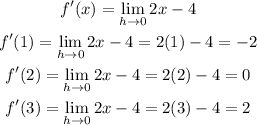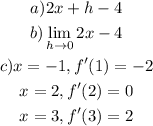
1) Considering that quadratic equation, we can find and simplify this expression that presents the limit of this function as h approaches 0.

a)

`\begin{gathered} (f(x+h)-f(x))/(h)= \\ ((x+h)^2-4(x+h)+1-(x^2-4x+1))/(h) \\ (x^2+2xh+h^2-4x+4h+1-x^2+4x-1)/(h) \\ (2xh+h^2-4h)/(h) \\ (h\left(2x+h-4\right))/(h) \\ 2x+h-4 \end{gathered}`

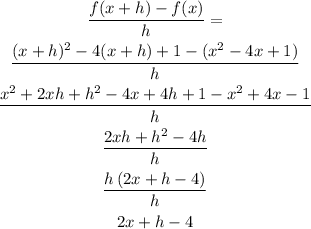
b) When h becomes very close to zero, we can find this:

`\begin{gathered} 2x+0-4 \\ 2x-4 \end{gathered}`

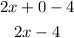
In other words, we find the limit of this function (or the first derivative) as h approaches 0.

c) Let's use this simplified expression to find the instantaneous rate of change at x=1,x=2, and x=3

`\begin{gathered} f^(\prime)(x)=\lim _(h\to0)2x-4 \\ f^(\prime)(1)=\lim _(h\to0)2x-4=2(1)-4=-2 \\ f^(\prime)(2)=\lim _(h\to0)2x-4=2(2)-4=0 \\ f^(\prime)(3)=\lim _(h\to0)2x-4=2(3)-4=2 \end{gathered}`