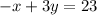Question

Write an equation In standard form using the information given.

Answer 1

Given the line

`y=3x-5`

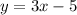
That has slope m=3 and y-intercept b=-5

You have to determine the equation of a line that passes through the point (8,5) and is:

a) Parallel to the given line.

If both lines are parallel, then they have the same slope, so, for the parallel line that passes through the point (8,5) the slope is also m=3

Using the point-slope form you can determine the equation as:

`y-y_1=m(x-x_1)`

Where (x₁,y₁) are the coordinates of the point the line is supposed to cross

Replace the formula with the slope and the coordinates of the point:

`y-5=3(x-8)`

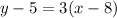
Next, you have to express it in standard form: Ax+By=C

To do so you have to solve the multiplication to the parentheses term on the right side of the formula. Use the distributive property of multiplications to do so:

`\begin{gathered} y-5=3x-3\cdot8 \\ y-5=3x-24 \end{gathered}`

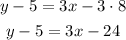
Next, pass "-5" to the right side of the equation and "3x" to the left side by applying the inverse operations:

`\begin{gathered} y-5+5=3x-24+5 \\ y=3x-19 \\ y-3x=-19 \end{gathered}`

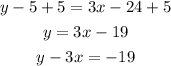
So the equation in the standard form of a line parallel to y=3x-5 that passes through the point (8,5) is

`-3x+y=-19`

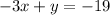
b) Perpendicular to the given line.

When two lines are perpendicular, the slopes are reverse reciprocals, that is, one is the inverse negative of the other:

`m_2=-(1)/(m_1)`

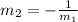
The slope of the given line is m=3, then the slope of a line perpendicular to it will be:

`m=-(1)/(3)`

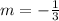
Now that we have determined the slope, using the point-slope form you can determine the equation of the perpendicular line that passes through the point (8,5):

`\begin{gathered} y-y_1=m(x-x_1) \\ y-5=-(1)/(3)(x-8) \end{gathered}`

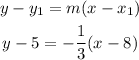
Now you have to follow the same steps as before. First, solve the multiplication on the parentheses term:

`\begin{gathered} y-5=-(1)/(3)x+(-(1)/(3))(-8) \\ y-5=-(1)/(3)x+(8)/(3) \end{gathered}`

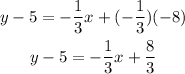
Second, pass the x term to the left side and the constant to the right side by applying the inverse operation to the expression:

`\begin{gathered} y-5+5=-(1)/(3)x+(8)/(3)+5 \\ y=-(1)/(3)x+(23)/(3) \\ y-(1)/(3)x=(23)/(3) \end{gathered}`

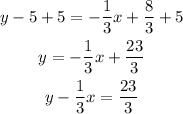
Rearrange the terms and multiply the whole expression by 3 to cancel the fractions:

`\begin{gathered} 3(-(1)/(3)x+y)=3((23)/(3)) \\ 3(-(1)/(3)x)+3y=3((23)/(3)) \\ -x+3y=23 \end{gathered}`

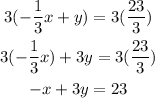
So the equation in the standard form of a line perpendicular to y=3x-5 and passes through the point (8,5) is

`-x+3y=23`