Question

The function f(t) = 4 cos(pi over 3t) + 15 represents the tide in Bright Sea. It has a maximum of 19 feet when time (t) is 0 and a minimum of 11 feet. The sea repeats this cycle every 6 hours. After five hours, how high is the tide?

Answer 1

f(5)=4 cos( 5π3)+ 15=17

Hope this helps

Tide is 17 ft

Answer 2

Answer with explanation:

The Cosine function which represents the tide in Bright Sea is represented as:

`f(t)=4 cos((\pi)/(3t)) + 15 \\\\ f(t)=4 cos(2 k\pi+(\pi)/(3t)) + 15`

Where, k=0,1,2,3,...........

Cos function has a Period of
`2\pi`.

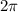Maximum , Cosine of an angle =1

Minimum, Cosine of an Angle = -1

At, t=0, →Maximum ,f(t)= 4 ×1 +15=19 feet

Minimum, f(t)= 4 × (-1) +15=15-4=11 feet

Tide repeats after ,every 6 hours.

After , 6 hours ,the tide function is represented in same way.That is

`f(t)=4 cos(2 k\pi + (\pi)/(3t)) + 15`

Here,k=6 n, where, n=0,1,2,3...

We have to find how tide function is represented after 5 hours.

→ 6 n=5

→
`n=(5)/(6)`

`f(t)=4 cos(2*(5*\pi)/(6) + (\pi)/(3* 5)) + 15\\\\f(t)=4 cos((5*\pi)/(3)+ (\pi)/(15))+15\\\\f(t)=4* cos((26\pi)/(15))+15\\\\f(t)=4 * cos 312^(\circ)+15\\\\f(t)=4* cos 48^(\circ)+15\\\\ f(t)=4 * 0.6691+15\\\\f(t)=2.6764+15\\\\f(t)=17.68`

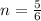
Height of tide after 5 hours = 17.68 feet