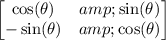Hello there. In order to reflect the point across the x-axis, we have to remember some properties about reflections on the cartesian plane.
Given the cartesian plane and the point (4, -7) as follows:
You want to determine a point that has the same distance from the x-axis in the opposite quadrant to it.
In this case, the point is in the fourth quadrant and reflecting across the x-axis, you find that the point must be in the first quadrant.
Another thing that will happen is that the point will have the same x-coordinate, hence you only have to determine the y-coordinate.
Having the same x-coordinate means that the point are lined with respect to the vertical line x.
Hence the coordinate of the point is simply: (x, -y).
In our case, we get
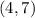
This is the point we get by reflecting it across the x-axis:
Another way of finding it is by applying the rotation matrix transformation: