The population growth in this question is assumed to be exponential.
The exponential formula is given to be:
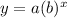
where a is the initial amount and b is the growth rate of the population.
The question provides the following parameters:
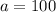
We can find the growth rate by making the following substitution: If there were 230 insects after 7 days, we have:
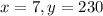
Therefore,
![\begin{gathered} 230=100(b)^7 \\ b^7=2.3 \\ b=\sqrt[7]{2.3} \\ b=1.126 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/35k4mevo1bxkswmqf8ll.png)
Therefore, the exponential model for the problem is:
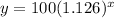
To find the time it takes for the population to reach 600 insects, we can substitute for y = 600 into the model and solve for x:
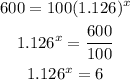
Finding the natural logarithm of both sides:
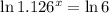
Recall the law of logarithms:
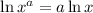
Therefore,
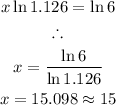
Therefore, it will take 15 days for the insect population to reach 600 insects.