Question

A farmer has 40 metres of fencing to build a rectangular pen for his prize-winning pigs. If the width of the pen is W metres, what is the greatest area that can be enclosed? Solve using quadratic relations.

Answer 1

Given that

A farmer has 40 meters of fencing to build a rectangular pen for his prize-winning pigs. If the width of the pen is W meters.

Explanation -

We have to find the greatest area that can be enclosed with this fencing.

The width of the pen is W and the fencing is 40 meters.

So its perimeter is 40 meters.

Let the length of the pen will be L then,

Perimeter = 2 (l + b)

40 = 2(l + W)

40/2 = l + W

l + W = 20

l = 20 - W

So the length is (20 - W) meters.

Now we have to find the area then,

`\begin{gathered} Area=l* b \\ A=(20-W)* W \\ Area=20W-W^2 \end{gathered}`

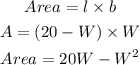
Final answer -

So the maximum area that can be enclosed will be 20W - W^2.