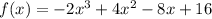Question

Find an nth-degree polynomial function with real coefficients satisfying the given conditions. If you are using a graphing utility, use it to graph the function and verifythe real zeros and the given function value.n = 3;2 and 2 i are zeros;f(-1)=30f(x) =(Type an expression using x as the variable. Simplify your answer.)Help me solve this►View an example Get more helpClear allCheck answerCopyright © 2022 Pearson Education Inc. All rights reserved. Terms of Use | Privacy Policy | Permissions | Contact UCon

Answer 1

We need to find a polynomial function f(x) with degree 3 and zeros 2 and 2i, such that:

`f(-1)=30`

Since 2i is a zero, -2i is also a zero of this function. Thus, we have:

`f(x)=a(x-2)(x-2\imaginaryI)(x+2\imaginaryI)`

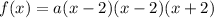
where a is a constant.

Expanding the expression on the right side, we obtain:

Now, using f(-1) = 30, we obtain:

`\begin{gathered} 30=a\lbrack(-1)³-2(-1)²+4(-1)-8\rbrack \\ \\ 30=a(-1-2-4-8) \\ \\ 30=a(-15) \\ \\ a=(30)/(-15) \\ \\ a=-2 \end{gathered}`

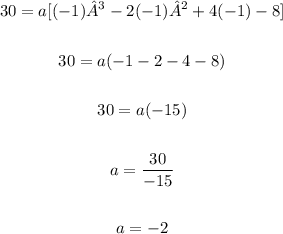
Therefore, the function is:

Answer

`f(x)=-2x^(3)+4x^(2)-8x+16`