Question

A laptop computer is purchased for $3200. Each year, its value is 80% of its value the year before. After how many years will the laptop computer be worth $700 or less? (Use the calculator provided if necessary.)Write the smallest possible whole number answer.

Answer 1

we know that

Each year, its value is 80% of its value the year before

that is the same as

Each year the value decreases by 20%

we have an exponential decay function of the form

`y=a(1-r)^x`

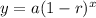
where

y is the value of the computer laptop

x is the number of years

r is the rate

a is the initial value

so

we have

a=$3,200

r=20%=20/100=0.20

substitute

`\begin{gathered} y=3,200(1-0.20)^x \\ y=3,200(0.80)^x \end{gathered}`

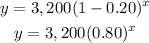
For y=$700

substitute in the equation above

`\begin{gathered} 700=3,200(0.80)^x \\ solve\text{ for x} \\ (700)/(3,200)=(0.80)^x \end{gathered}`

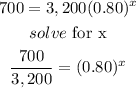
Apply log on both sides

`\begin{gathered} log((700)/(3,200))=x*log(0.80) \\ x=6.81\text{ years} \end{gathered}`

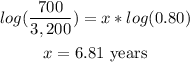
therefore

The answer is 7 years