Question

I'm kind of confused on this one I got some help but I'm still struggling to figure it out

Answer 1

`f(x)=5x^2+5x-30`

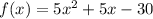
Step-by-step explanation

Step 1

the standard form of a quadratic equation is given by

`f(x)=ax^2+bx+c`

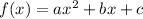
then, by the table, we have:

`y=f(x)`

`\begin{gathered} f(x)=ax^2+bx+c \\ f(-4)=a(-4)^2+b(-4)+c \\ f(-4)\rightarrow30=16a-4b+c\rightarrow\text{Equation}(1) \\ f(-3)=a(-3)^2+b(-3)+c \\ f(-3)=9a+-3b+c \\ f(3)=0=9a+-3b+c\rightarrow\text{Equation}(2) \\ \end{gathered}`

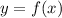
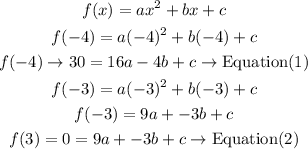
now, we have 2 equations, and 3 variables ( a, b and c, so we need one more equation)

when x= 2

`\begin{gathered} f(x)=ax^2+bx+c \\ f(2)=0=a2^2+b\cdot2+c \\ f(2)=0=4a+2b+c\rightarrow Equation\text{ (3)} \end{gathered}`

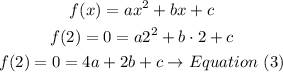
Step 3

solve the equations

`\begin{gathered} 30=16a-4b+c\rightarrow\text{Equation}(1) \\ 0=9a-3b+c\rightarrow\text{Equation}(2) \\ 0=4a+2b+c\rightarrow Equation\text{ (3)} \end{gathered}`
`\begin{gathered} 0(eq2)=0(eq3) \\ \text{9a-}3b+c=4a+2b+c \\ \text{subtract c in both sides} \\ \text{9a-}3b+c-c=4a+2b+c-c \\ \text{9a-}3b=4a+2b \\ \text{subtract 4a in both sides} \\ \text{9a-}3b-4a=4a+2b-4a \\ 5a-3b=2b \\ \text{add 3b in both sides} \\ 5a-3b+3b=2b+3b \\ 5a=5b \\ \text{divide both sides by 5} \\ (5a)/(5)=(5b)/(5) \\ a=b \end{gathered}`

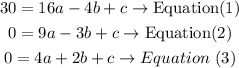
Now, replace a=b in equation (1) and equation (2)

`\begin{gathered} 30=16a-4b+c\rightarrow\text{Equation}(1) \\ 30=16a-4a+c \\ 30=12a+c\rightarrow\rightarrow equation\text{ (4)} \\ 0=9a-3b+c\rightarrow\text{Equation}(2) \\ 0=9a-3a+c \\ 0=6a+c\rightarrow\rightarrow equation(5) \end{gathered}`

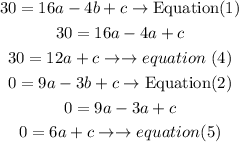
Step 3

use equations (4) and (5) to find a and c

`\begin{gathered} 30=12a+c\rightarrow\rightarrow equation\text{ (4)} \\ 0=6a+c\rightarrow\rightarrow equation(5) \end{gathered}`

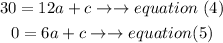
a)isolate c in both equations and equal the expressions to find a

`\begin{gathered} 30=12a+c\rightarrow\rightarrow equation\text{ (4)} \\ 30-12a=c \\ c=30-12a \\ 0=6a+c\rightarrow\rightarrow equation(5) \\ -6a=c \\ c=c \\ 30-12a=-6a \\ \text{add 6a in both sides} \\ 30-12a+6a=-6a+6a \\ 30-6a=0 \\ \text{subtract 30 in both sides} \\ 30-6a-30=0-30 \\ -6a=-30 \\ \text{divide both sides by -6} \\ (-6a)/(-6)=(-30)/(-6) \\ a=5 \end{gathered}`

we have a= 5,

now, replace in equation (4) to find x

`\begin{gathered} 30=12a+c\rightarrow\rightarrow equation\text{ (4)} \\ 30=12\cdot5+c \\ 30=60+c \\ \text{subtrac 60 in both sides } \\ 30-60=60+c-60 \\ -30=c \\ c=-30 \end{gathered}`

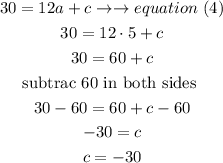
Therefore we have

a=5 b=5 c=-30

Step 4

finally, rewrite the equation

`\begin{gathered} f(x)=ax^2+bx+c \\ f(x)=5x^2+5x-30 \end{gathered}`

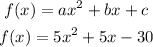
I hope this helps you