Question

You pour yourself a cold glass (m = 0.6 kg) of ice tea (m = 1.2 kg) on a hot summer day andaccidently leave it in the sun, which causes both the tea and the glass to warm up to atemperature of 19°C. You want to bring it down both down to a nice cold 1°C before you drinkit. What mass of ice at -15°C do you need to add to the system to cool it down? Assume, thespecific heat of water and tea is 4186 J/kg°C, the specific heat of the cup is 837 J/kg°C, thespecific of ice is 2090 J/kg°C, and the latent heat of fusion for ice to water is 3.34 x 105 J/kg.

Answer 1

`\begin{equation*} 0.269kg=269g \end{equation*}`

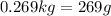
Step-by-step explanation

Parameters given:

Mass of glass, mg = 0.6 kg

Mass of ice tea, mt = 1.2 kg

Temperature of tea and glass = Tg = Tt = T1 = 19°C

Required temperature, T2 = 1°C

Temperature of ice, Ti = -15°C

The sum of the heat lost by the glass and the heat lost by the tea must be equal to the heat gained by the ice:

`m_gc_g(T_1-T_2)+m_tc_t(T_1-T_2)=H_i`

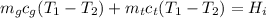
where cg = specific heat of the cup.

ct = specific heat capacity of the tea

Hi = heat gained by ice

The heat gained by ice is given as the sum of the heat gained to convert the ice to ice at 0°C, the heat gained to convert the ice at 0°C to water at 0°C and the heat gained to convert water at 0°C to water at 1°C:

`H_i=mc_i(T_0-T_(-15))+mL_f+mc_w(T_1-T_0)_`

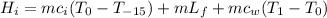
where ci = specific heat capacity of ice

Lf = latent heat of fusion of ice

Therefore, we can substitute this into the original formula:

`m_gc_g(T_1-T_2)+m_tc_t(T_1-T_2)=mc_i(T_0-T_(-15))+mL_f+mc_w(T_1-T_0)_`

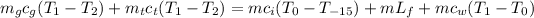
Solving for m in the equation above, the mass of ice needed is:

That is the mass of ice needed.