Question

Elizabeth brought a box of donuts to share. There are two-dozen (24) donuts in the box, all identical in size, shape, and color. Two are jelly-filled, 9 are lemon-filled,and 13 are custard-lilled. You randomly select one donut, eat it, and select another donut. Find the probability of selecting a jelly-filled donut followed by acustard-filled donut(Typo an Integer or a simplified fraction)Time Remaining: 00:47:06

Answer 1

Step-by-step explanation

So there are 24 donuts in the box with 3 different fillings. The probability of selecting a a jelly-filled donut first is given by the following quotient:

`\frac{\text{number of jelly-filled donuts remaining}}{\text{ total number of donuts remaining}}`

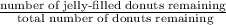
Since this is the first donut there are 2 jelly-filled donuts out of a total of 24. Then the probability of selecting a jelly-filled donut first is:

`P_1=(2)/(24)=(1)/(12)`

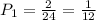
In a similar way we can find the probability of selecting a a custard-filled donut after selecting a jelly-filled donut in the first place. After the first selection we have 13 custard-filled donuts out of a total of 23 since one was already taken. Then this probability is:

`P_2=(13)/(23)`

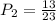
Finally, the probability of selecting a jelly-filled donut followed by a custard-filled donut is given by the product of the two probabilities we found:

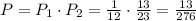
`P=P_1\cdot P_2=(1)/(12)\cdot(13)/(23)=(13)/(276)`Answer

Then the answer is 13/276.