Question

Write the equation in slope-intercept form through the point (-4, -7) and is perpendicular to the line y = -(7/4)x + 4 and graph.

Answer 1

You have to write the equation for a line that crosses the point (-4, -7) and is perpendicular to the line

`y=-(7)/(4)x+4`

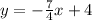
When you have to determine a line that is perpendicular to a known line, you have to keep in mind that the slope of the perpendicular line will be the negative inverse of the first one.

If for exampla you have two lines, the first one being:

`y_1=mx+b`

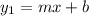
And the second one, that is perpedicular to the one above:

`y_2=nx+c`

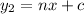
The slope of the second one is the negative inverse of the first one:

`n=-(1)/(m)`

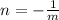
The slope of the given line y=-7/4+4 is m=-7/4

So the slope of the perpendicular line has to ve the inverse negative of -7/4

`\begin{gathered} n=-(-(4)/(7)) \\ n=(4)/(7) \end{gathered}`

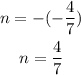
Considering it has to pass through the point (-4,-7) and that we already determined its slope, you can unse the point slope formula to determine the equation of the perpendicular line:

`y-y_1=m(x-x_1)`

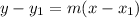
replace with the coordinates of the point and the slope and calculate:

`\begin{gathered} y-(-7)=(4)/(7)(x-(-4)) \\ y+7=(4)/(7)(x+4) \\ y+7=(4)/(7)x+(16)/(7) \end{gathered}`

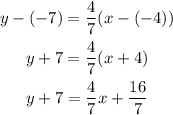
Subtract 7 to both sides of the equation to write it in slope-intercept form:

`\begin{gathered} y+7-7=(4)/(7)x+(16)/(7)-7 \\ y=(4)/(7)x-(33)/(7) \end{gathered}`

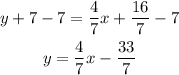
Now you can graph both lines