Given the figure of a circle
As shown, there are two chords UT and CV that intersection at point W
The length of the chords are as follows:
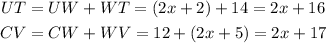
And there is a relation between the chords that are as follows:
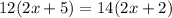
We will solve the last equation to find the value of x:

Substitute x = 8 into the expressions of UT and CV:

So, the value of UT + CV = 32 + 33 = 65
So, the answer will be D. 65