Question

Two airlines leave the airport. Plane A departs at a 41° angle from the runway, and plane B departs at a 43° angle from the runway. Which plane was farther away from the airport when it was 5 miles from the ground? Round the solution to the nearest hundredth.

Answer 1

Given that Plane A departs at a 41° angle from the runway while plane B departs at a 43° angle from the runway.

h stands for the height of the planes above the ground

x stands for the distance of plane A away from the airport.

y stands for the distance of plane A away from the airport.

When h = 5, we shall calculate their respective x

`\begin{gathered} \text{ For Plane A} \\ \sin 41^0=(h)/(x)\Rightarrow x=(h)/(\sin 41^0) \\ \Rightarrow x=(5)/(\sin41^0)=7.62\text{ miles} \\ \text{ For Plane B} \\ \sin 43^0=(h)/(y)\Rightarrow y=(h)/(\sin43^0) \\ \Rightarrow y=(5)/(\sin43^0)=7.33\text{ miles} \end{gathered}`

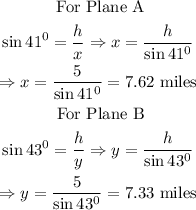
From the above calculation, we can see that Plane A what 7.62 miles away from the airport while Plane B was 7.33 miles away from the airport.

Since 7.62 > 7.33;

Therefore, Plane A was farther away from the airport when it was 5 miles from the ground.