Question

a) Test the claim that males and females have the same meanbody mass index (BMI). What are the null and alternativehypotheses?b) The test statistic, t, is ____ (round to two decimal places as needed.)c) The P-value is ____(round to three decimal places as needed.)d) State the conclusion for the test.A. Fail to reject the null hypothesis. There is sufficientevidence to warrant rejection of the claim that men andwomen have the same mean BMI.B. Reject the null hypothesis. There is not sufficientevidence to warrant rejection of the claim that men andwomen have the same mean BMI.C. Fail to reject the null hypothesis. There is not sufficientevidence to warrant rejection of the claim that men andwomen have the same mean BMI.D. Reject the null hypothesis. There is sufficient evidenceto warrant rejection of the claim that men and women havethe same mean BMI.e) Construct a confidence interval suitable for testing theclaim that males and females have the same mean BMI.____<μ1-μ2<____(round to three decimal places as needed.)f) Does the confidence interval support the conclusion of thetest?

Answer 1

Given the question in the image, the following are the solution to the questions:

a. null hypothesis

`H_(\circ)\colon\mu_1=\mu_2`

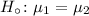
alternative hypothesis

`H_1\colon\mu_1\\e\mu_2`

Question b: To get the test statistic, t

`\begin{gathered} t=\frac{(X_1-X_(2))-(\mu_1-\mu_2)_{}_{}}{\sqrt[\square]{(s_(1^2))/(n_1)-(s_(2^2))/(n_2)_{}}} \\ \text{Since }\mu_1=\mu_(2,)difference=0 \\ t=\frac{(27.1141-26.3239)}{\sqrt[\square]{(7.687374^2)/(50)+(5.039494^2)/(50)}} \\ t=\frac{0.7902}{\sqrt[\square]{1.18191-0.50793}} \\ t=(0.7902)/(0.67398) \\ t=1.1724 \\ t\approx1.17 \end{gathered}`

Question c: To get the P-value from T score with 0.05 significance level and two tailed hypotheses:

`\begin{gathered} \text{ Using the P-value calculator, the P-value equals:} \\ P-value=0.246705 \\ P-\text{value}\approx0.247 \end{gathered}`

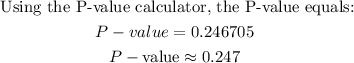
Question d: Conclusion for the test:

Since the P-value is greater than the significance level (0.05), then the correct option is C. Fail to reject the null hypothesis. There is not sufficient evidence to warrant rejection of the claim that men and women have the same mean BMI.

Question e: