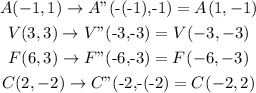Question

Rotation 180° CW about the origin of AVFC some help would be nice

Answer 1

A'' = (1, -1)

V'' = (-3, -3)

F'' = (-6, -3)

C'' = (-2, 2)

Explanations:

Given the coordinate of the quadrilateral AVFC as shown:

A = (-1, 1)

V = (3, 3)

F = (6, 3)

C =(2, -2)

The rule for the 180° clockwise rotation about the origin is given as;

`(x,y)\rightarrow(-x,-y)`

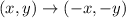
This shows that the coordinates were negated but their original position must be retained.

For the coordinate points of the quadrilateral AVFC, the 180° clockwise rotation about the origin will be given as;

`\begin{gathered} A(-1,1)\rightarrow A\text{''(-(-1),-1)}=A^(\doubleprime)(1,-1) \\ V(3,3)\rightarrow V\text{''(-3,-3)}=V^(\doubleprime)(-3,-3) \\ F(6,3)\rightarrow F\text{''(-6,-3)}=F^(\doubleprime)(-6,-3) \\ C(2,-2)\rightarrow C\text{''(-2,-(-2)}=C^(\doubleprime)(-2,2) \end{gathered}`