The first thing we have to do is derivate the function in order to obtain the critical points of the function. Then we'll check which of them are inflection points, maximum or minimum.
So we have:
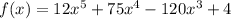
Derivating:
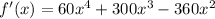
To obtain the critical points we equal this derivate to cero:
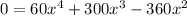
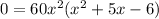
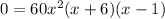
From this factor expression we can determinate the possible solutions is:
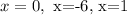
Then we have 3 critical points.
To determinate what are they, if they are inflection, maximum or minimum and the concave of the intervales we have to do the cementery law, if you don't know about it don't worry, It is just evaluate the derivate:
Untill now we have this information:
As we said before, we have to evaluate in each intervale, if the values is negative then it means that the function is decreasing, if it is positive the function is increasing. We can use any value of each intervale.
To the first intervale we will use -10, to do the operation easier.
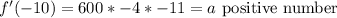
To the second intervale we will use -1:
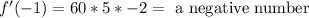
To the third intervale we will use 0.5:
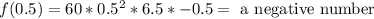
To the last intervale we will use 10:
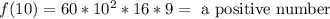
From this we can conclude that the critical points are x=-6, x=-1, x=0.
And the direction of the function, if it is increasing or decreasing.
To get the concavity of the function we use the second derivate criterion:
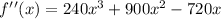
We equal to cero this time again:
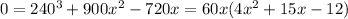
From this we obtain the inflection points:
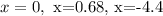
Now we evaluate in the intervarles:
To the first interval we will use -10:
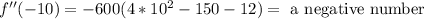
To the second interval we will use -1:
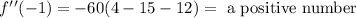
To the third interval we will use 0.5:
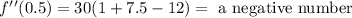
To the last interval we will use 1:
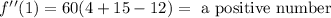
If the value of evaluate the second derivate is positve then the fuction is concave up, if the value is negative is concave down.
We can conclude:
The inflection points are:
x=-4.4
x=0
x=0.68
Concavity:
(-∞,-4.4)= concave down
(-4.4,0)= concave up
(0,0.68)= concave down
(0.68,∞)=concave up