Question

Question is attachedSelect all that apply1.The graph of g(x) is shifted seven units to the left of f(x)2. The graph of g(x) is shifted seven units to the right of f(x)3. The graph of g(x) is shifted seven units above f(x)4. The graph of g(x) is shifted seven units below f(x)5. The vertex of g(x) is (7,0)6. The axis of symmetry of g(x) is x=0

Answer 1

We are given the following function:

`f(x)=x^2-5`

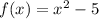
We are also given the following function:

`g(x)=f(x-7)`

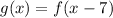
This means that the value of the function "g(x)" is obtained by substituting the value of "x" is "f(x)" for "x-7", like this:

`g(x)=(x-7)^2-5`

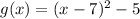
This type of transformation is a translation 7 units to the right, therefore, the graph of g(x) is shifted 7 units to the right of f(x).

The function is of the form:

`g(x)=a(x-h)^2+k`

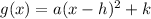
Where the vertex of the function is:

`(x,y)=(h,k)`

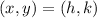
Therefore, the vertex of the function is:

`(x,y)=(7,-5)`

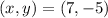
And the axis of symmetry is the x-coordinate of the vertex, therefore, the axis of symmetry is:

`x=7`

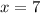
This means that the statements that apply is 2