Question

A car has an initial velocity of 41.79 m/s. It then accelerates at a uniform rate of 6.53 m/s² for the next 13.73 seconds. What would the distance covered be if the car started from rest and accelerated in the time period above?

Answer 1

We are given that a car starts moving from rest and reaches a velocity of 41.79 m/s. Then it accelerates at a rate of 6.53 m/s² for 13.73 seconds. We are asked to determine the distance traveled if the initial velocity is zero. First, we will determine the final velocity of the car. To do that we will use the following equation of motion for constant acceleration:

`v_f=v_0+at`

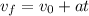
Where:

`\begin{gathered} v_f=\text{ final velocity} \\ v_0=\text{ initial velocity} \\ a=\text{ acceleration} \\ t=\text{ time} \end{gathered}`

Since we are told that the car starts from rest this means that the initial velocity is zero and also initially accelerates in the same time period this means that the time is "t = 13.73 seconds". Replacing in the formula we get:

`v_f=at`

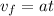
Replacing the values:

`v_f=(6.53(m)/(s^2))(13.73s)`

Solving the operations:

`89.66\frac{m}{s^{}}=v_f`

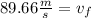
Now we use the following equation of motion to determine the distance traveled:

`2ax=v^2_f-v^2_0`

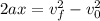
Where:

`x=\text{ distance traveled}`

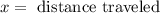
Now we solve for the distance "x" by dividing both sides by "2a":

`a=(v^2_f-v^2_0)/(2a)`

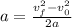
Replacing the values we get:

`x=((89.66(m)/(s))^2)/(2(6.53(m)/(s^2)))`

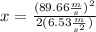
Solving the operations we get:

`x=615.5m`

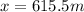
Therefore, the distance traveled is 615.5 meters.