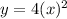Question

Derive the equation of the parabola with a focus at (0, 1) and a directrix of y = −1. (2 points)

Answer 1

warning, it is NOT f(x)= 4x^2, I got a 0 on the question for putting in that answer. my best guess is that they forgot the negative sign? so I would try the f(x)= -4x^2 option instead, hope it works out

Answer 2

`y=4(x)^2`

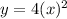
Explanation:

Focus =(h,k+p)

Directrix= y=k-p

Focus given is : (0,1)

And directrix given is : y=-1

(h,k+p) =(0,1)

On comparing the values we get

h=0 and k+p=1

y=k-p= -1

Hence, we gave two equations

k+p=1 and k-p= -1

Substitute p= 1-k in k-p= -1 we get:

k-(1-k) = -1

k-1+k= -1

k=0

Now, we get

h=0 and k=0

And put k=0 in p = 1-k

We get p=1

We have general equation of parabola

`(y-k)=4p(x-h)^2`

`(y-0)=4(1)(x-0)^2`

`y=4(x)^2`

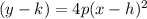
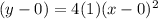
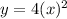
Hence, the required equation is :

`y=4(x)^2`