Step-by-step explanation
Let's recall that to reflect a polygon it is sufficient to reflect its vertices. After reflecting them, we only need to join the resulting points by segments to get the reflection of the total quadrilateral.
With this in mind, let's reflect the four vertices of our figure over the given line.
Let's start with
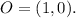
Firstly, we need to find the perpendicular line passing through O. It has the equation
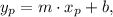
where m is the slope, and b is the y-intercept. For we want the line to be perpendicular to the given one, we have
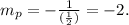
Then, the equation above becomes
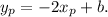
Now, O must lie in the line; then, ("we can evaluate the equation for O")
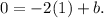
Solving it for b, we get
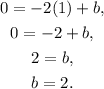
Thus, the equation for the line perpendicular to the given one passing through O is
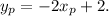
Let's graph our current situation:
The green line represents the given line, and the blue line represents the perpendicular line, which equation we just found. Point B is the point where both lines intersect. The reflection of O over the provided line is point C, the point on the perpendicular line which is "as far from B as O".
Now, How to calculate C? Note that B is the middle point between C and O. Then, if
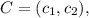
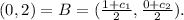
That is
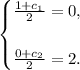
Solving both equations, we get
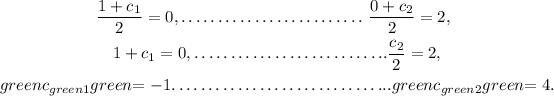
Thus
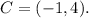
Repeating this process to the remaining vertices, we get that the reflection of
F is (-8,3), the reflection of T is (-5,7), and the reflection of R is (4,9).
Let's graph what we have obtained:
It only remains to apply the idea given in the first paragraph.
Answer