Question

I saw these answers by the community on here, but they don’t explain how they got the answers. I need help with why 2, 4, and 5 are the answers because I know why 1 is an answer.

Answer 1

Given:

`\begin{gathered} SQ=10cm \\ \angle PCQ=30^(\circ) \end{gathered}`

To find:

The correct statements

Step-by-step explanation:

Since the angles PCQ and SCR are vertically opposite angles.

So, we can write it as,

`\begin{gathered} \angle PCQ=\angle SCR \\ \hat{PQ}=\hat{SR} \end{gathered}`

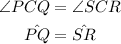
Therefore, the arc PQ is congruent to arc SR.

So, the first statement is correct.

Since the angles PCQ and SCR are vertically opposite angles and the angles QCR and PCS are vertically opposite angles.

So, we can write it as,

Since the central angle of a circle is 360 degrees.

Therefore,

`\begin{gathered} \hat{PQ}+\hat{QR}+\hat{RS}+\hat{PS}=360 \\ 30+\hat{QR}+30+\hat{PS}=360 \\ \hat{QR}+\hat{PS}=360-60 \\ \hat{QR}+\hat{QR}=300[QR\text{ and PS are vertical angles\rbrack} \\ 2\hat{QR}=300 \\ \hat{QR}=150^(\circ) \end{gathered}`

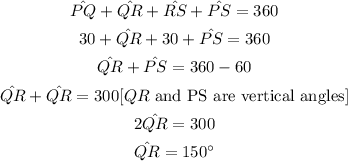
Therefore, the measure of an arc QR is 150 degrees.

So, the second statement is correct.

Let us find the circumference of the circle.

`\begin{gathered} Radius=(10)/(2)cm \\ r=5cm \end{gathered}`

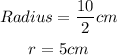
Using the circumference formula,

`\begin{gathered} C=2\pi r \\ =2*\pi*5 \\ =10\pi cm \end{gathered}`

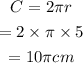
Therefore, the circumference of the circle is,

`C=10\pi cm`

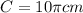
So, the third statement is wrong.

Let us find the arc length of PS.

Here,

`\begin{gathered} Radius,r=(10)/(2) \\ r=5cm \\ \hat{PS}=150^(\circ) \end{gathered}`

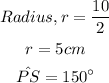
Using the formula,

`\begin{gathered} l=(\theta)/(360)*2\pi r \\ Arc\text{ length, }\hat{PS}=(150)/(360)*2*(22)/(7)*5 \\ =13.09 \\ \approx13.1cm \end{gathered}`

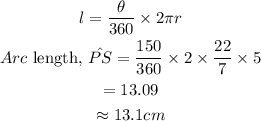
Therefore, the arc length of PS is 13.1cm.

So, the fourth statement is correct.

Let us find the arc length of QS.

Here,

`\begin{gathered} r=5cm \\ \hat{QS}=P\hat{Q}+\hat{PS} \\ =30+150 \\ \hat{QS}=180^(\circ) \end{gathered}`

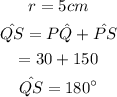
Using the formula,

`\begin{gathered} l=(\theta)/(360)*2\pi r \\ Arc\text{ length, }\hat{QS}=(180)/(360)*2*(22)/(7)*5 \\ =15.71 \\ \approx15.7cm \end{gathered}`

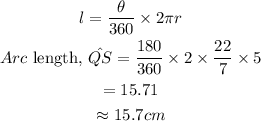
Therefore, the arc length of QS is 15.7cm.

So, the fifth statement is correct.

Final answer: The statements 1, 2, 4, and 5 are correct.