Question

Suppose the vertex of a parabola is in the first quadrant and the parabola opens upwards. What can be determined about the value of a and the discriminant?

Answer 1

A parabola is the graph of a quadratic function,

that is the graph of
`f(x)=a x^(2) +bx+c`, where a is not 0.

from a, b and c we can derive the following informations about the shape of a parabola:

if a>0, the parabola opens upwards.
if a<0, the parabola opens downwards.

Consider the discriminant
`D= b^(2) -4ac`

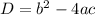
If D>0, the parabola intersects the x-axis at 2 points.
If D=0, the parabola intersects the x-axis at 1 point.
If D<0, the parabola does not intersect the x axis.

"the vertex of a parabola is in the first quadrant and the parabola opens upwards."

the vertex is in the first quadrant means that the vertex is above the x-axis, and it opens upwards, so the parabola does not intersect the x-axis.

This means that:

Answer: a>0, the discriminant D<0