Let:
q be the number of quarters
d be the number of dimes
To solve this question, follow the steps below.
Step 01: Write an equation that relates the number of quarters and dimes.
Knowing that "The number of quarters was 12 more than three times the number of dimes":
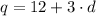
Step 02: Write an equation that shows the amount of money that Peter has.
Dime = 10 cents = $0.10.
Quarter = 25 cents = $0.25.
Then,
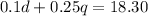
Step 03: Substitute q from step 1 in the equation from step 02.
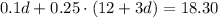
And solve the equation for d.
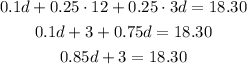
Subtracting 3 from both sides:
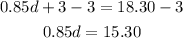
And divide both sides by 0.85:
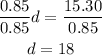
The number of dimes is 18.
Step 04: Knowing the number of dimes, find the number of quarters.
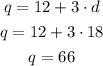
The number of quarters is 66.
In summary,
Number of dimes = 18.
Number of quarters = 66.