We are given 8 items. And we want to calculate all possible ways in which we can arrange these items. As we have 5 appetizers and 3 main courses. We can picture this situation as we have 8 boxes.
in each box, we are going to place on item and not take it out. We are told that the appetizers should go first. So, in the first 5 boxes we must put the appetizers and then in the rest we should put the main courses.
To calculate the number of possible ways of arranging the items, we will simply use the multiplication principle, which is: We will count the number of possibilities that we have to fill one box and then multiply all those numbers.
For the first first box, we have a total of 5 available options. Once we fill the first box, we have 4 options to fill the second box. If we continue in this matter, we have 3 options for box 3, 2 options for box 4 and 1 option for box 5. So this means that the total number of ways we can arrange 5 appetizers would be
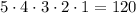
Now, we can do the same for boxes 6-8. For box 6, we have 3 options, for box 7 we have 2 options and for box 8 we have 1 option. So the total number of ways we can arrange the 3 main courses is
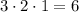
Now, note that for each way you arrange the first boxes, we have 6 possibilities of arranging the last three boxes. This means that the total number of ways of arranging the 8 items would be
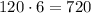
so there are 720 ways of arranging the 8 items