Question

The length of a rectangle is 7 inches more than its width. The area of the rectangle is equal to 2 inches less than 5 times the perimeter . What is the length and width

Answer 1

Let the width be w, then the length is w+7 units.

The area of the rectangle is
`A=w(w+7)= w^(2)+7w`.

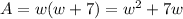
The perimeter of the rectangle is:

P = 2(Width + Length)=2(w+w+7)=2(2w+7)=4w+14

"The area of the rectangle is equal to 2 inches less than 5 times the perimeter." means that:

A = 5P - 2


`w^(2)+7w=5(4w+14)-2`


`w^(2)+7w=20w+70-2`


`w^(2)-13w-68=0`

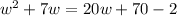
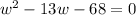
to solve the quadratic equation, let's use the quadratic formula

let a=1, b=-13, c=-68


`D= b^(2) -4ac=169-4(1)(-68)=169+272=441`

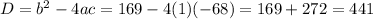
the root of the discriminant is 21

the roots are

w1=(13+21)/2=34/2=17
and
w2=(13-21)/2=-8/2=-4, which cannot be the width.

The width is 17 units, and the length is 17+7=24 units


Answer: w=17, l=24