Question

Apply the Pythagorean Theorem to find the distance between points A and B.A)V60 unitsB)768 unitsC)9 unitsD10 units

Answer 1

We can form a right triangle with the segments AC (one of the legs), BC (the other leg), and AB (the hypotenuse).

The Pythagorean theorem states:

`c^2=a^2+b^2`

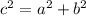
where a and b are the legs and c is the hypotenuse of a right triangle.

From the graph, the length of AC is 8 units, and the length of BC is 2 units. Substituting in the Pythagorean theorem we get:

`\begin{gathered} AB^2=AC^2+BC^2 \\ AB^2=8^2+2^2 \\ AB^2=64+4 \\ AB^2=68 \\ AB=\sqrt[]{68}\text{ units} \end{gathered}`