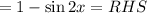Question

Prove the identity: (cosx-sinx)^2 = 1-sin2x

Answer 1

Given the identity:

`(\cos x-\sin x)^2=1-\sin 2x`

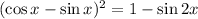
The proof of the identity will be as follows:

We will begin from the left-hand side by expanding the square

`LHS=(\cos x-\sin x)^2=\cos ^2x-2\sin x\cos x+\sin ^2x`

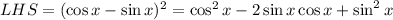
Combine the first and the last terms, which will be the Pythagorean identity

`\begin{gathered} =(\sin ^2x+\cos ^2x)-2\sin x\cos x \\ =1-2\sin x\cos x \end{gathered}`

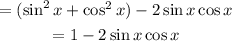
Note, note the last term (2 sin x cos x) = sin 2x

So,

`\begin{gathered} =1-\sin 2x=R\mathrm{}H\mathrm{}S \\ \end{gathered}`