Question

(08.06)The following data show the height, in inches, of 11 different garden gnomes:

2 9 1 23 3 7 10 2 10 9 7
After removing the outlier, what does the mean absolute deviation of this data set represent?
On average, the height of a garden gnome varies 3.2 inches from the mean of 7 inches.
On average, the height of a garden gnome varies 3.6 inches from the mean of 6 inches.
On average, the height of a garden gnome varies 3.2 inches from the mean of 6 inches.
On average, the height of a garden gnome varies 3.6 inches from the mean of 7 inches.

Answer 1

Answer: Please don’t judge me but I agree with the other guy, it’s (C.
Credits to him ♥️

Answer 2

The correct statement is:

On average, the height of a garden gnome varies 3.2 inches from the mean of 6 inches.

Explanation:

We are given a data of 11 gardens as:

2 9 1 23 3 7 10 2 10 9 7

Now on removing the outlier i.e. 23 (since it is the very large value as compared to other data points) the entries are as follows:

x |x-x'|

2 4

9 3

1 5

3 3

7 1

10 4

2 4

10 4

9 3

7 1

Now mean of the data is denoted by x' and is calculated as:

`x'=(2+9+1+3+7+10+2+10+9+7)/(10)\\\\x'=(60)/(10)\\\\x'=6`

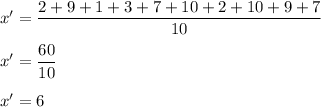
Hence, Mean(x')=6

Now,

∑ |x-x'|=32

Now mean of the absolute deviation is:

`(32)/(10)=3.2`

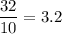
This means that , On average, the height of a garden gnome varies 3.2 inches from the mean of 6 inches.