Question

A horizontal pipe of diameter 0.926 m hasa smooth constriction to a section of diameter0.5556 m. The density of oil fowing in thepipe is 821 kg/ m3If the pressure in the pipe is 7920 N/m? andin the constricted section is 5940 N/m?, whatis the rate at which oil is flowing?Answer in units of m°/s.

Answer 1

Use Bernoulli's principle to find a relation between the pressures of the liquid at each point of the pipe with the velocity of the fluid at the same locations:

`P_1+(1)/(2)\rho v^2_1=P_2+(1)/(2)\rho v^2_2`

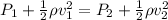
bring velocities to the left member of the equation and everything else to the right member of the equation:

`\begin{gathered} \Rightarrow(1)/(2)\rho v^2_1-(1)/(2)\rho v^2_2=P_2-P_1_{}^{} \\ \Rightarrow(1)/(2)\rho(v^2_1-v^2_2)=P_2-P_1_{}_{} \\ \Rightarrow v^2_1-v^2_2=(2(P_2-P_1))/(\rho) \end{gathered}`

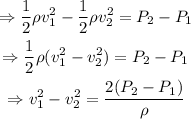
Use the continuity equation to relate the velocities of the fluid at each point of the pipe with the cross-sectional area of the pipe at those locations:

Notice that we have found two equations with two unknowns (the velocities of the fluid at points 1 and 2).

We can use the continuity equation to eliminate one unkown in the Bernoulli's Principle, then we can find the value of one of the velocities. Next, simply multiply the speed of the fluid at one location of the pipe times the cross-sectional area of the pipe at that point to find the rate Φ at which the oil is flowing:

`\Phi=A\cdot v`

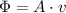
Isolate v₂ from the continuity equation:

`v_2=(A_1)/(A_2)v_1`

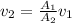
Since the cross-sectional area is proportional to the square of the diameter of the pipe, then:

`v_2=(D^2_1)/(D^2_2)v_1`

Replace this expression for v₂ into Bernoulli's Principle and isolate v₁:

`\begin{gathered} v^2_1-v^2_2=\frac{2(P_2-P_1)^{}}{\rho} \\ \Rightarrow v^2_1-((D^2_1)/(D^2_2)v_1)^2=(2(P_2-P_1))/(\rho) \\ \Rightarrow v^2_1-(D^4_1)/(D^4_2)v^2_1=(2(P_2-P_1))/(\rho) \\ \Rightarrow(1-(D^4_1)/(D^4_2))v^2_1=(2(P_2-P_1))/(\rho) \\ \Rightarrow v^2_1=(2(P_2-P_1))/(\rho(1-(D^4_1)/(D^4_2))) \\ \Rightarrow v^{}_1=\sqrt[]{(2(P_2-P_1))/(\rho(1-(D^4_1)/(D^4_2)))} \\ \\ \therefore v^{}_1=\sqrt[]{(2(P_2-P_1))/(\rho(1-(D^4_1)/(D^4_2)))} \end{gathered}`

The area of a circle with diameter D is given by:

`A=(\pi D^2)/(4)`

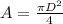
Then, the rate at which the oil is flowing as a function of the known variables, is:

`\begin{gathered} \Phi=A_1v_1 \\ =(\pi D^2_1)/(4)\cdot\sqrt[]{(2(P_2-P_1))/(\rho(1-(D^4_1)/(D^4_2)))} \\ =(\pi)/(4)\cdot\sqrt[]{(2(P_2-P_1))/((\rho)/(D^4_1)(1-(D^4_1)/(D^4_2)))} \\ =(\pi)/(4)\cdot\sqrt[]{(2(P_2-P_1))/(\rho((1)/(D^4_1)-(1)/(D^4_2)))} \\ \\ \therefore\Phi=(\pi)/(4)\cdot\sqrt[]{(2(P_2-P_1))/(\rho((1)/(D^4_1)-(1)/(D^4_2)))} \end{gathered}`

Replace the pressures P₁=7920N/m^2, P₂=5940N/m^2, the density ρ=821kg/m^3, and the corresponding diameters D₁=0.926m and D₂=0.5556m to find the rate at which the oil is flowing:

`\begin{gathered} \Phi=(\pi)/(4)\cdot\sqrt[]{\frac{2(\lbrack5940(N)/(m^2)\rbrack-\lbrack7920(N)/(m^2)\rbrack)}{\lbrack821(kg)/(m^3)\rbrack((1)/(\lbrack0.926m\rbrack^4)-\frac{1}{\lbrack0.5556m\rbrack^4_{}})}}=0.5707302986\ldots(m^3)/(s) \\ \\ \therefore\Phi\approx0.571(m^3)/(s) \end{gathered}`

Therefore, the rate at which the oil is flowing, is 0.571 cubic meters per second.