Answer:
Option B is correct.
(1 , -5) lies on the graph.
Explanation:
Given the points (4,1) and (-2 , -11)
First find the linear equation for the given points.
Equation of line for two points
 and
and
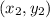
is given by:
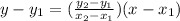
Substitute the given points (4,1) and (-2 , -11) in above equation to find the equation of line:

or
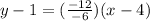
or
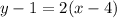
Using distributive property on RHS ( i.e,
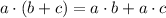 )
)
we have;
y -1 = 2x-8
Add 1 to both sides of an equation;
y-1+1 = 2x-8+1
Simplify:
y = 2x -7
Therefore, the equation of line for the given point is: y =2x - 7 ....[1]
To find which points lies on the graph ( i.e, Line)
Substituting the given options in equation [1] we have;
A . (1,1)
Put x =1 and y =1
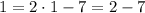
1 = -5 which is not true.
Similarly
B. for (1, -5)

-5 = -5 which is true.
C. for (1, 2)

2 = -5 which is not true.
And
D. For (1 , -7)

-7 = -5 which is also not true.
Therefore, the only point which lies on the line graph [1] is; (1 ,-5)