Question

What's the balance (to the nearest cent) after 11 yr if you invest $700 at a nominal annual rate of 4.5% if:

Answer 1

Given that the investment money is $700. The nominal annual interest rate is 4.5% and the time period is 11 years.

We have to find the amount at given time period.

a)

The formula when the interest is compounded annually is:

`A=P(1+r)^t`

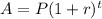
Substitute the given values in the formula:

`\begin{gathered} A=700(1+0.045)^(11) \\ =700(1.623) \\ =1136.1 \end{gathered}`

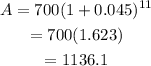
Thus, the answer is $1136.1.

b)

The formula of amount when the interest is compounded weekly is:

`A=P(1+(7r)/(365))^{(365)/(7)t}`

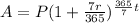
Substitute the given values in the formula:

`\begin{gathered} A=700(1+(7*0.045)/(365))^{(365*11)/(7)} \\ =700(1+0.000863)^(573.57) \\ =700(1.000863)^(573.57) \\ =700(1.6401) \\ =1148.07 \end{gathered}`

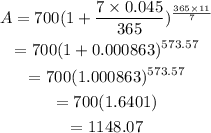
Thus, the answer is $1148.07.

c)

The formula of amount when the interest is compounded daily is:

`A=P(1+(r)/(365))^(365t)`

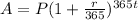
Substitute the given values in the formula:

`\begin{gathered} A=700(1+(0.045)/(365))^(365*11) \\ =700(1+0.0001232)^(4015) \\ =700(1.0001232)^(4015) \\ =700(1.6398) \\ =1147.86 \end{gathered}`

Thus, the answer is $1147.86.

d)

The formula when the interest is compounded continuously is:

`A=Pe^(rt)`

substitute the given values in the formula:

`\begin{gathered} A=700e^((0.045*11)) \\ =700e^(0.495) \\ =700(1.6404) \\ =1148.28 \end{gathered}`

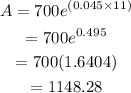
Thus, the answer is $1148.28.