Question

8. An ellipse has a vertex at (4,0), a co-vertex at (0, 3), and a center at the origin. Which is the equation of the ellipse in standard form?916

Answer 1

By definition, the Standard form of the equation of an ellipse is:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

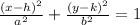
Where the center is:

`(h,k)`

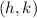
When its center is at the Origin, the equation is:

`(x^2)/(a^2)+\frac{y^2^{}}{b^2}=1`

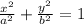
When:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

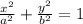
Where:

`a>b`

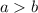
It is horizontal.

And when:

`(x^2)/(b^2)+(y^2)/(a^2)=1`

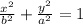
Where:

`a>b`

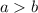
It is vertical.

In this case, you know that this ellipse is centered at the Origin, its vertex is:

`(4,0)`

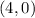
And the co-vertex is at:

`(0,3)`

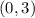
Analyzing the information given in the exercise, you can idenfity that:

`\begin{gathered} a=4 \\ b=3 \end{gathered}`

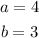
Therefore, you can substitute values into the equation

`(x^2)/(a^2)+(y^2)/(b^2)=1`

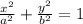
You get:

`\begin{gathered} (x^2)/(4^2)+(y^2)/(3^2)^{}=1 \\ \\ (x^2)/(16)+(y^2)/(9)^{}=1 \end{gathered}`

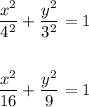
The answer is: Last option.