Question

Which is the first step?Evaluate the first equation for x = -5.O Evaluate the second equation for x = -1.O Evaluate the second equation for x = 5.O Evaluate the first equation for x = -1.

Answer 1

Step-by-step explanation

A piecewise function formed by two equations with domains a≤x

In this case the two equations are:

`\begin{gathered} f(x)=2x+3n \\ h(x)=2x^2-3x-9 \end{gathered}`

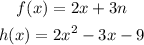
They are both polynomials so we know they are continuous in their respective domains. Then we just need to compare the values of f and h at x=-1 which is the value where their domains meet. Then the first step would be evaluating the first equation at x=-1:

`f(-1)=2\cdot(-1)+3n=-2+3n`

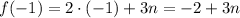
Then we evaluate the second equation at x=-1:

`\begin{gathered} h(-1)=2\cdot(-1)^2-3\cdot(-1)-9 \\ h(-1)=-4 \end{gathered}`

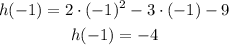
Then we have to look for the value of n that makes h(-1)=f(-1). Then we equalize these two results:

`-2+3n=-4`

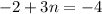
And we solve this equation for n. We can start by adding 2 to both sides:

`\begin{gathered} -2+3n+2=-4+2 \\ 3n=-2 \end{gathered}`

And we divide both sides by 3:

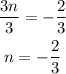
`\begin{gathered} (3n)/(3)=-(2)/(3) \\ n=-(2)/(3) \end{gathered}`Answer

The first step to find n is evaluating the first equation for x=-1. Then the answer is the fourth option.