Hello there. To solve this question, we'll have to remember some properties about law of sines and cosines.
Given a triangle ΔABC, that is, with sides a, b and c and angles A, B and C opposite to the respective letter's side, as in the following drawing:
When we have some informations about the measures of the sides of the triangle and angles, we can determine the missing information depending on the combination of the information.
If we have one side and two angles in a triangle, that is exactly the case we're interested into, we can:
Determine the missing angle by subtracting the sum of the two others from 180º, knowing that the sum of the internal angles of a triangle is equal to 180º.
After this, we still have only one side of the triangle, so we would want to find the measure of the two other sides.
Since we know all the angles, we can apply the law of sines, that statement's precisely: The ratio between the sides of a triangle and the sine of the respective angle opposite to the sides is equal to a constant. (in fact, the diameter of the circle we inscribe the triangle).
The constant part makes sure the ratio between any side of the triangle and the sine of the opposite angle to this side is equal to all sides and angles, or mathematically:
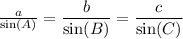
So we can calculate it twice and determine the measure of the missing sides, therefore solving the triangle.
The answer to this question is: yes. and it is contained in the first option.