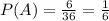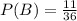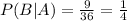Question

A pair of fair dice is tossed.  Let A = {the sum is 7} and B = {3 appears on at least one die}Find each of the following.  Write your answer as a fraction.P(A) = P(B) = P(A∩B)=P(B | A) = P(A | B) =

Answer 1

To find the probability we need to count each one of the cases.

The event A is the sum of the dices are 7, since the dices are distinguishable between them we have that the event A is the set:

`A=\lbrace(6,1),(5,2),(4,3),(3.4),(2.5),(1,6)\}`

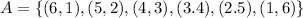
Now the event B is the set:

`B=\lbrace(3,1),(3.2),(3,3),(3,4),(3,5),(3,6),(1,3),(2.3),(4,3),(5,3),(6,3)\}`

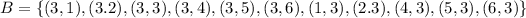
Now that we have our sets A and B we can calculate the other ones:

`A\cap B=\lbrace(4,3),(3,4)\}`
`B|A=\lbrace(3,1),(3,2),(3,3),(3,5),(3,6),(1,3),(2,3),(5,3),(6,3)\}`
`A|B=\lbrace(6,1),(5,2),(2,5),(1,6)\}`

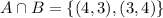
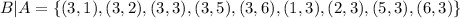
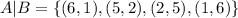
Now that we have all our sets we have to count how many cases each of them have and divided them by the total number os possible outcomes (36).

Then:

`P(A)=(6)/(36)=(1)/(6)`
`P(B)=(11)/(36)`
`P(A\cap B)=(2)/(36)=(1)/(18)`
`P(B|A)=(9)/(36)=(1)/(4)`
`P(A|B)=(4)/(36)=(1)/(9)`