Question

Which function represents transforming f(x)=3^x with a reflection over the x-axis and a vertical shift of 4 units? 3^x+ 4, -3^x+ 4, 3^x-4, -3^x+4

Answer 1

the -3 reflects over the x axis and + 4 gives vertical shift of 4 units
Its option D.

Answer 2

Answer:
`-3^x +4`

Explanation:

The equation for the vertical reflection of a function f(x) across the x-axis is given by :-

`y=-f(x)`

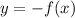
The vertical shift of 'k' units of a function g(x) is given by :-

`y=g(x)+k`

Now, the equation for the vertical reflection of a function
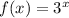`f(x)=3^x` across the x-axis is given by :-

`-f(x)=-3^x`

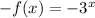
Then , the equation for the vertical shift of 4 units of function
`-3^x` is given by :-

`y=-3^x +4`

Hence, the function represents transforming
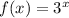`f(x)=3^x` with a reflection over the x-axis and a vertical shift of 4 units

`y=-3^x +4`