Question

Looking to receive full help on this practice question, thank you! Looking for this to be graphed.

Answer 1

Step-by-step explanation: Here we can see that all the options (graphs) have their own vertex (minimum or maximum value for the function) which means that once we find the vertex of our function we will already be able to choose the correct answer.

Below we have a generic form for a quadratic function and the formula to find the x-coordinate of the vertex

`\begin{gathered} y=ax^2+bx+c \\ Vertex_(x-coordinate)=(-b)/(2a) \end{gathered}`

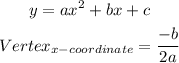
Step 1: Let's simplify our equation to get a generic form as follows

`\begin{gathered} y=2(x+3)^2-3 \\ y=2(x+3)(x+3)^{}-3 \\ y=2(x^2+6x+9)-3 \\ y=2x^2+12x+15 \end{gathered}`

We can see above that

`\begin{gathered} a=2 \\ b=12 \\ c=15 \end{gathered}`

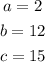
Step 2: Now we can calculate the vertex as follows

`\begin{gathered} Vertex_(x-coordinate)=(-b)/(2a) \\ Vertex_(x-coordinate)=(-12)/(2\cdot2) \\ Vertex_(x-coordinate)=(-12)/(4) \\ Vertex_(x-coordinate)=-3 \end{gathered}`

Above we got the x-coordinate for the vertex.

Step 3: Now we just need to substitute x = -3 on our equation to find the y-coordinate of the vertex

`\begin{gathered} y=2x^2+12x+15 \\ \text{if x = -3 then } \\ y=2(-3)^2+12(-3)+15 \\ y=-3 \end{gathered}`

Step 4: Now we know that our vertex is placed in the point (-3,-3). There is another thing that will help us to understand our function. Looking at the coefficient "a" we have that if a < 0 so the concavity is facing downwards but if a>0 it means that the concavity is facing up. As we can see a = 2 > 0 so our concavity is facing up.

Step 5: Now we can illustrate a draft of our function with vertex (-3,-3) and with the concavity facing up as follows

Final answer: As we can see the second option (graph) is the only graph that matches the concavity and vertex of our function so the second graph is the final answer.