Question

Identify the vertex intercepts and whether of the graph of the function below opens up or downAnswers as a point (x,y).

Answer 1

Absolute value functions:

`\begin{gathered} f(x)=a\lvert x-h\rvert+k \\ \\ \text{Vertex:} \\ (h,k) \end{gathered}`

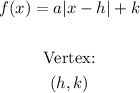
Given function:

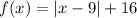
`f(x)=\lvert x-9\rvert+16`Vertex: (9,16)

x-intercept: Point where the graph cross the x-axis (when f(x)=0)

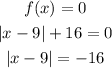
`\begin{gathered} f(x)=0 \\ \lvert x-9\rvert+16=0 \\ \lvert x-9\rvert=-16 \\ \end{gathered}`As any absolute value is negative the function has no x-intercept.

y-intercept: Point where the graph cross the y-axis (when x=0)

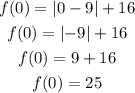
`\begin{gathered} f(0)=\lvert0-9\rvert+16 \\ f(0)=\lvert-9\rvert+16 \\ f(0)=9+16 \\ f(0)=25 \end{gathered}`y-intercept: (0,25)

The graph opens up if a>0 and opens down if a<0

In the given function a=1

The graph opens up