To find the probability between two z-scores on a normal distribution, we can use a z-score table.
A z-score table gives the probability of a data less than the corresponding z-score, like in the picture:
So, if we want the probability between 1.98 and -1.15, we need to do the following:
![P(-1.15However, usually z-score tables go only from z = 0 and above, so we need a way to consult the negative <em>z</em>.<p>Since the normal distribution in symmetric around z = 0, we have that:</p>[tex]P(z<-1.15)=P(z>1.15)]()
And since the whole distribution give a 100% probability, or an area of 1, we have that:
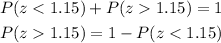
So, in the end, we have:
![\begin{gathered} P(-1.151.15) \\ P(-1.15So, we can consult the values for the probabilities of z < 1.98 and z < 1.15 on the z-score table:[tex]\begin{gathered} P(z<1.98)\approx0.9761 \\ P(z<1.15)\approx0.8749 \end{gathered}]()
So, the total probability is:
[tex]\begin{gathered} P(-1.15So, the probability is
approximately 0.8510.