Question

A yo-yo is thrown toward the ground with an initial velocity of -4 feet per second. Its velocity v in feet per second t seconds after being thrown is given by v = 4t − 4, where t runs from 0 to 2 seconds. Find the times for which the yo-yo's velocity is greater than 2 feet per second or less than −2 feet per second. Express your answer as decimals.

Answer 1

Given the equation that represents this situation:

`\begin{gathered} v(t)=4t-4 \\ t\in\lbrack0,2\rbrack \end{gathered}`

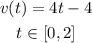
first, if we want to know when the yo-yo's velocity is greater than 2 feet per second, then:

`\begin{gathered} v(t)>2 \\ \Rightarrow4t-4>2 \\ \Rightarrow4t>2+4=6 \\ \Rightarrow t>(6)/(4)=(3)/(2)=1.5 \\ t>1.5 \end{gathered}`

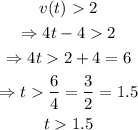
since t is defined between 0 and 2, the times for which the yoyo's velocity is greater than 2 feet per second is:

`1.5then, if we suppose that the velocity is less than -2 feet per second, then:[tex]\begin{gathered} v(t)<-2 \\ \Rightarrow4t-4<-2 \\ \Rightarrow4t<-2+4=2 \\ \Rightarrow t<(2)/(4)=(1)/(2)=0.5 \\ t<0.5 \end{gathered}`

then, we have that the interval is:

`0\le t<0.5`