Given the figure of a cone inside a cylinder
The volume of the space between the cylinder and the cone = the volume of the cylinder - the volume of the cone
The volume of the cylinder =
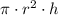
The volume of the cone =
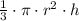
So, the volume of the space between them =
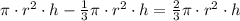
As shown in the figure: r = 4/2 = 2 in
h = 6 in
Let pi = 3.14
So, substitute with r, h, and pi
The volume of the space =
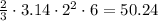
Rounding to the nearest whole number
So, the answer will be option B) 50 in^3